Time Series Forecasting Lab (Part 6)

Cover photo by Markus Spiske on Unsplash

Go to R-bloggers for R news and tutorials contributed by hundreds of R bloggers.

Introduction

This is the sixth of a series of 6 articles about time series forecasting with panel data and ensemble stacking with R.

Through these articles I will be putting into practice what I have learned from the Business Science University training course 1 DS4B 203-R: High-Performance Time Series Forecasting", delivered by Matt Dancho. If you are looking to gain a high level of expertise in time series with R I strongly recommend this course.

The objective of this article is to learn how to build multi-level stacking ensembles with modeltime. In the figure below we start from the bottom by reminding us of each individual model or submodel performance from Part 4 (non-tuned models) and Part 5 (tuned models). Then we will define meta learners which learn from k-fold cross-validation predictions from all submodels. We can compare meta-learners' performance and select best meta-learners to be used for defining a weighted average ensemble to produce a final multi-level stacking model.

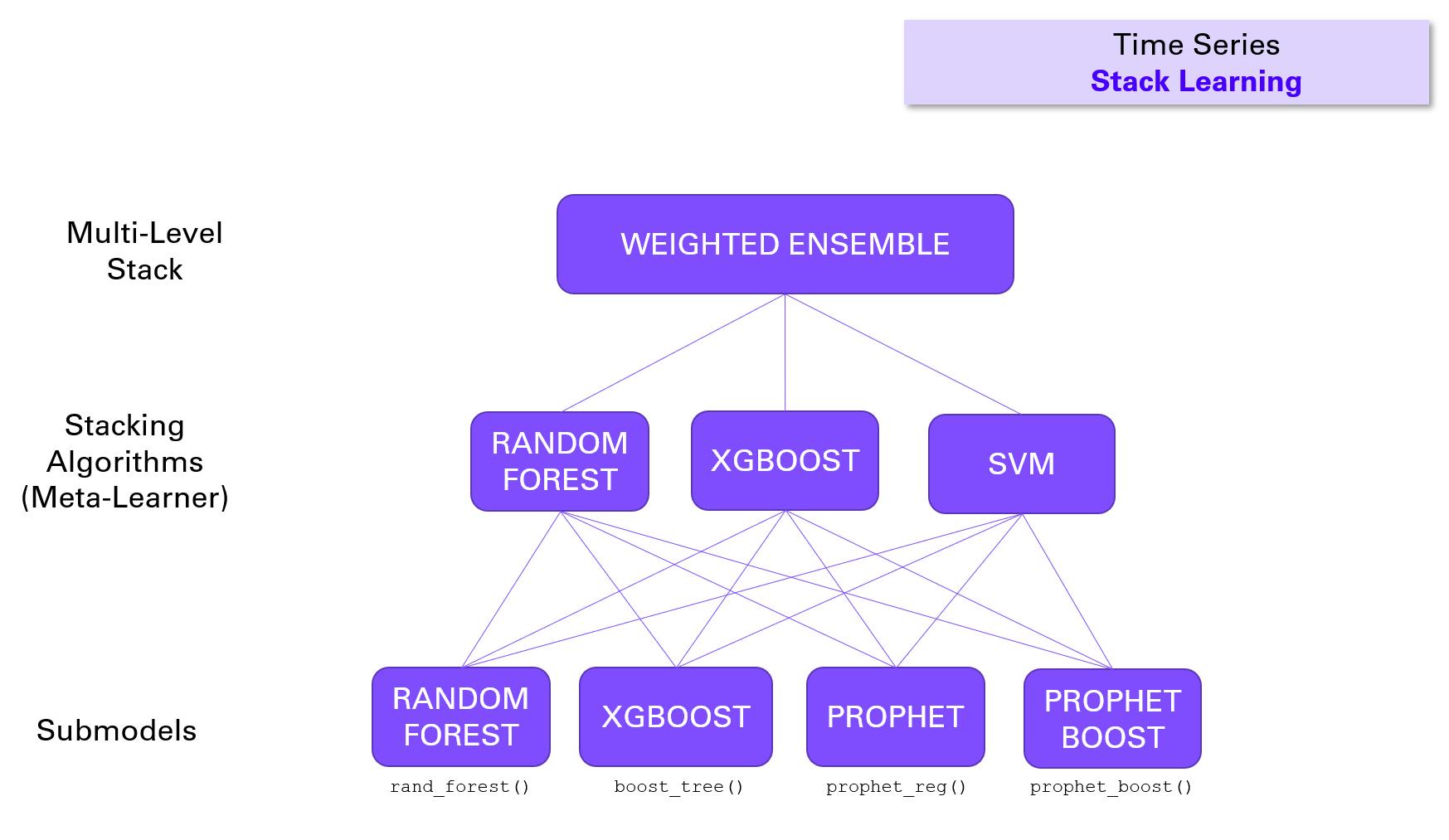
Prerequisites

I assume you are already familiar with the following topics, packages and terms:

dplyr or tidyverse R packages
k-fold cross-validation
hyperparameter tuning from Part 4
average and weighted ensembles from Part 5

Packages

The following packages must be loaded:

# 01 FEATURE ENGINEERING
library(tidyverse)  # loading dplyr, tibble, ggplot2, .. dependencies
library(timetk)  # using timetk plotting, diagnostics and augment operations
library(tsibble)  # for month to Date conversion
library(tsibbledata)  # for aus_retail dataset
library(fastDummies)  # for dummyfying categorical variables
library(skimr) # for quick statistics

# 02 FEATURE ENGINEERING WITH RECIPES
library(tidymodels) # with workflow dependency

# 03 MACHINE LEARNING
library(modeltime) # ML models specifications and engines
library(tictoc) # measure training elapsed time

# 04 HYPERPARAMETER TUNING
library(future)
library(doFuture)
library(plotly)

# 05 ENSEMBLES
library(modeltime.ensemble)

Reminder of individual models

Leu us remind us of the performance of each individual model or submodel. We do not consider the ensemble models from Part 5.

# Load all calibration tables (tuned & non-tuned models)
> calibration_tbl <- read_rds("workflows_NonandTuned_artifacts_list.rds")
> calibration_tbl <- calibration_tbl$calibration
> calibration_tbl %>% 
   modeltime_accuracy() %>%
   arrange(rmse)

# A tibble: 8 x 9
  .model_id .model_desc                       .type   mae  mape  mase smape  rmse   rsq
      <int> <chr>                             <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1         7 PROPHET W/ REGRESSORS             Test  0.189  21.6 0.417  21.5 0.240 0.856
2         3 PROPHET W/ REGRESSORS - Tuned     Test  0.189  21.6 0.418  21.5 0.241 0.857
3         4 PROPHET W/ XGBOOST ERRORS - Tuned Test  0.191  25.7 0.421  19.9 0.253 0.780
4         8 PROPHET W/ XGBOOST ERRORS         Test  0.204  24.8 0.451  20.8 0.287 0.753
5         2 XGBOOST - Tuned                   Test  0.219  23.6 0.482  22.9 0.296 0.762
6         6 XGBOOST                           Test  0.216  25.0 0.476  22.4 0.299 0.747
7         1 RANGER - Tuned                    Test  0.231  26.1 0.509  24.6 0.303 0.766
8         5 RANGER                            Test  0.235  25.4 0.519  25.0 0.312 0.765

Stacking Algorithms

A stacking algorithm or meta-learner learns from predictions. The predictions come from k-fold cross-validations applied to each submodel. Once fed into the meta-learner tunable specification a hyperpameter tuning will be peformed for the meta-learner.

Generate predictions for meta-learners

Remember, for non-sequential models you must perform a k-fold cross-validation and not a time series cross-validation. Let us get resampeld predictions with modeltime_fit_resamples(). Here, k=10 folds.

set.seed(123)
resamples_kfold <- training(splits) %>%
  drop_na() %>%
  vfold_cv(v = 10)

tic()
submodels_resamples_kfold_tbl <- calibration_tbl %>%
  modeltime_fit_resamples(
    resamples = resamples_kfold,
    control   = control_resamples(
      verbose    = TRUE, 
      allow_par  = TRUE,
    )
  )
toc()

Setup parallel processing

Parallel processing is set and toggled on by running the following commands:

# Parallel Processing ----
registerDoFuture()
n_cores <- parallel::detectCores()

plan(
  strategy = cluster,
  workers  = parallel::makeCluster(n_cores)
)

Meta-learners specification

In this article we will use 3 meta-learners: Random Forest, XGBoost, and SVM.

Create a stacking algorithm specification with ensemble_model_spec(). Within the meta-learner specification we must provide the tunable parameters, the number of folds, and the size of the grid. We will also set grid search control parameters by activating verbose and allowing parallel processing.

For all meta-learners specifications we will define a k=10 folds and a grid size of 20.

Random Forest stacking algorithm

We perform tuning on 2 parameters: mtry and min_n.

We notice that the in-sample RMSE for the meta-learner is 0.125. Its performance on test data has RMSE = 0.230 and RSQ = 0.817.

tic()
set.seed(123)
ensemble_fit_ranger_kfold <- submodels_resamples_kfold_tbl %>%
  ensemble_model_spec(
    model_spec = rand_forest(
      trees = tune(),
      min_n = tune()
    ) %>%
      set_engine("ranger"),
    kfolds  = 10, 
    grid    = 20,
    control = control_grid(verbose = TRUE, 
                           allow_par = TRUE)
  )
toc()

i Model Parameters:
# A tibble: 1 x 8
  trees min_n .metric .estimator  mean     n std_err .config              
  <int> <int> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
1  1906    32 rmse    standard   0.176    10 0.00225 Preprocessor1_Model02

i Prediction Error Comparison:
# A tibble: 9 x 3
  .model_id  rmse .model_desc                      
  <chr>     <dbl> <chr>                            
1 1         0.196 RANGER - Tuned                   
2 2         0.183 XGBOOST - Tuned                  
3 3         0.207 PROPHET W/ REGRESSORS - Tuned    
4 4         0.179 PROPHET W/ XGBOOST ERRORS - Tuned
5 5         0.203 RANGER                           
6 6         0.203 XGBOOST                          
7 7         0.208 PROPHET W/ REGRESSORS            
8 8         0.207 PROPHET W/ XGBOOST ERRORS        
9 ensemble  0.125 ENSEMBLE (MODEL SPEC)           

modeltime_table(
  ensemble_fit_xgboost_kfold
) %>%
  modeltime_accuracy(testing(splits))

# A tibble: 1 x 9
  .model_id .model_desc                       .type   mae  mape  mase smape  rmse   rsq
      <int> <chr>                             <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1         1 ENSEMBLE (RANGER STACK): 8 MODELS Test  0.166  21.8 0.367  18.2 0.230 0.817

XGBoost stacking algorithm

We perform tuning on 4 parameters: trees, tree_depth, learn_rate, loss_reduction.

We notice that the in-sample RMSE for the meta-learner is 0.0957. Its performance on test data RMSE = 0.251 and RSQ = 0.769.

tic()
set.seed(123)
ensemble_fit_xgboost_kfold <- submodels_resamples_kfold_tbl %>%
  ensemble_model_spec(
    model_spec = boost_tree(
      trees          = tune(),
      tree_depth     = tune(),
      learn_rate     = tune(),
      loss_reduction = tune()
    ) %>%
      set_engine("xgboost"),
    kfolds = 10, 
    grid   = 20, 
    control = control_grid(verbose = TRUE, 
                           allow_par = TRUE)
  )
toc()

# A tibble: 1 x 10
  trees tree_depth learn_rate loss_reduction .metric .estimator  mean     n std_err .config              
  <int>      <int>      <dbl>          <dbl> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
1  1717          8     0.0330        0.00876 rmse    standard   0.180    10 0.00175 Preprocessor1_Model10

i Prediction Error Comparison:
# A tibble: 9 x 3
  .model_id   rmse .model_desc                      
  <chr>      <dbl> <chr>                            
1 1         0.196  RANGER - Tuned                   
2 2         0.183  XGBOOST - Tuned                  
3 3         0.207  PROPHET W/ REGRESSORS - Tuned    
4 4         0.179  PROPHET W/ XGBOOST ERRORS - Tuned
5 5         0.203  RANGER                           
6 6         0.203  XGBOOST                          
7 7         0.208  PROPHET W/ REGRESSORS            
8 8         0.207  PROPHET W/ XGBOOST ERRORS        
9 ensemble  0.0957 ENSEMBLE (MODEL SPEC)  

> modeltime_table(
   ensemble_fit_xgboost_kfold
 ) %>%
   modeltime_accuracy(testing(splits))

# A tibble: 1 x 9
  .model_id .model_desc                        .type   mae  mape  mase smape  rmse   rsq
      <int> <chr>                              <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1         1 ENSEMBLE (XGBOOST STACK): 8 MODELS Test  0.182  23.9 0.401  19.7 0.251 0.769

SVM stacking algorithm

We perform tuning on 3 parameters: cost, rbf_sigma, margin. Run ?svm_rbf for explanations.

We notice that the in-sample RMSE for the meta-learner is 0.172. Its performance on test data RMSE = 0.219 and RSQ = 0.823.

tic()
set.seed(123)
ensemble_fit_svm_kfold <- submodels_resamples_kfold_tbl %>%
  ensemble_model_spec(
    model_spec = svm_rbf(
      mode      = "regression",
      cost      = tune(),
      rbf_sigma = tune(),  
      margin    = tune()
    ) %>%
      set_engine("kernlab"),
    kfold = 10, 
    grid  = 20, 
    control = control_grid(verbose = TRUE, 
                           allow_par = TRUE)
  )
toc()

# A tibble: 1 x 9
   cost rbf_sigma margin .metric .estimator  mean     n std_err .config              
  <dbl>     <dbl>  <dbl> <chr>   <chr>      <dbl> <int>   <dbl> <chr>                
1  4.60    0.0110 0.0595 rmse    standard   0.172    10 0.00222 Preprocessor1_Model07

i Prediction Error Comparison:
# A tibble: 9 x 3
  .model_id  rmse .model_desc                      
  <chr>     <dbl> <chr>                            
1 1         0.196 RANGER - Tuned                   
2 2         0.183 XGBOOST - Tuned                  
3 3         0.207 PROPHET W/ REGRESSORS - Tuned    
4 4         0.179 PROPHET W/ XGBOOST ERRORS - Tuned
5 5         0.203 RANGER                           
6 6         0.203 XGBOOST                          
7 7         0.208 PROPHET W/ REGRESSORS            
8 8         0.207 PROPHET W/ XGBOOST ERRORS        
9 ensemble  0.172 ENSEMBLE (MODEL SPEC)  

> modeltime_table(
   ensemble_fit_svm_kfold
 ) %>%
   modeltime_accuracy(testing(splits))

# A tibble: 1 x 9
  .model_id .model_desc                        .type   mae  mape  mase smape  rmse   rsq
      <int> <chr>                              <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1         1 ENSEMBLE (KERNLAB STACK): 8 MODELS Test  0.160  21.8 0.352  18.0 0.219 0.823

Multi-Level Stacks

The previous stacking approaches can be mutualized in a multi-level stack. We can combine meta-learners into a higher level of the stack which will be a normal (weighted) average ensemble as introduced in Part 5.

Below is a reminder of the previous stacking algorithms' performance:

modeltime_table(
  ensemble_fit_ranger_kfold, 
  ensemble_fit_xgboost_kfold,
  ensemble_fit_svm_kfold
) %>%
  modeltime_accuracy(testing(splits)) %>% 
  arrange(rmse)

# A tibble: 3 x 9
  .model_id .model_desc                        .type   mae  mape  mase smape  rmse   rsq
      <int> <chr>                              <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1         3 ENSEMBLE (KERNLAB STACK): 8 MODELS Test  0.160  21.8 0.352  18.0 0.219 0.823
2         1 ENSEMBLE (RANGER STACK): 8 MODELS  Test  0.166  21.8 0.367  18.2 0.230 0.817
3         2 ENSEMBLE (XGBOOST STACK): 8 MODELS Test  0.182  23.9 0.401  19.7 0.251 0.769

Let us now define a weighted average ensemble model from the stacking algorithms as we did in Part 5. We will apply the ranking technique to calculate the weights.

First we create the accuracy results table on which we apply the ranking technique for weigths calculation, then we create the weighted average ensemble model with ensemble_weighted() by applying the weights, and finally, we evaluate the model.

loadings_tbl <- modeltime_table(
  ensemble_fit_ranger_kfold, 
  ensemble_fit_xgboost_kfold,
  ensemble_fit_svm_kfold
) %>% 
  modeltime_calibrate(testing(splits)) %>%
  modeltime_accuracy() %>%
  mutate(rank = min_rank(-rmse)) %>%
  select(.model_id, rank)

stacking_fit_wt <- modeltime_table(
  ensemble_fit_ranger_kfold, 
  ensemble_fit_xgboost_kfold,
  ensemble_fit_svm_kfold
) %>%
  ensemble_weighted(loadings = loadings_tbl$rank)

> stacking_fit_wt  %>% 
   modeltime_calibrate(testing(splits)) %>%
   modeltime_accuracy() %>%
   arrange(rmse)
# A tibble: 1 x 9
  .model_id .model_desc                   .type   mae  mape  mase smape  rmse   rsq
      <int> <chr>                         <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1         1 ENSEMBLE (WEIGHTED): 3 MODELS Test  0.161  21.8 0.354  18.1 0.223 0.817

With RMSE = 0.223, the stacked ensemble algorithm outperformed all algorithms!

Forescast plot

Below the stacked ensemble algorithm's forecast plot on the test dataset for all industries, it looks good ! except for one industry the model seems to follow pretty well the trend and spikes of the actual data.

calibration_stacking <- stacking_fit_wt %>% 
  modeltime_table() %>%
  modeltime_calibrate(testing(splits))

calibration_stacking %>%
  modeltime_forecast(
    new_data    = testing(splits),
    actual_data = artifacts$data$data_prepared_tbl,
    keep_data   = TRUE 
  ) %>%
  group_by(Industry) %>%
  plot_modeltime_forecast(
    .facet_ncol         = 4, 
    .conf_interval_show = FALSE,
    .interactive        = TRUE,
    .title = "Forecast stacking level model (test data)"
  )

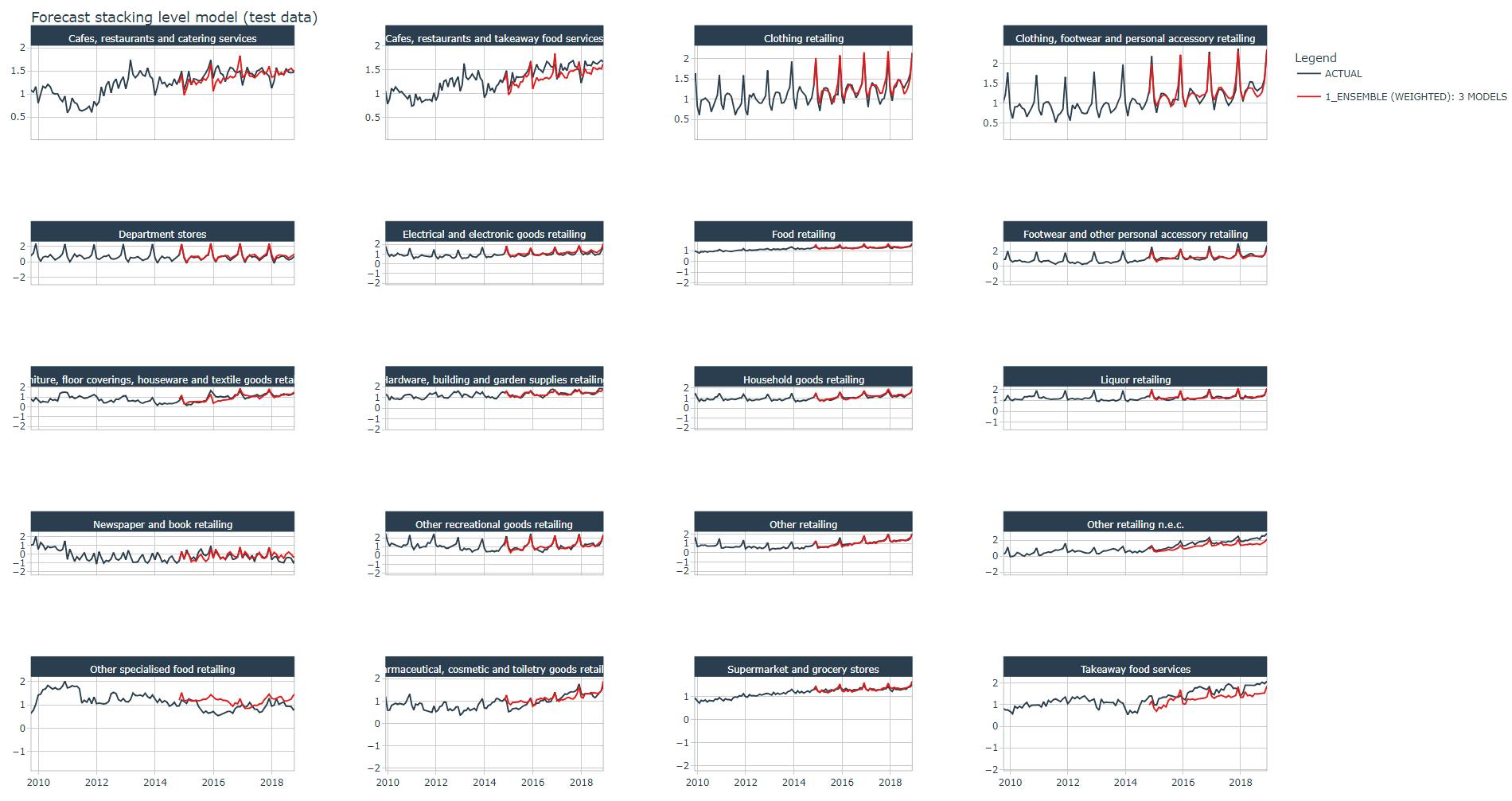
Next 12 months Turnover forecast

Let us now (finally!) perform the next 12 months Turnover forecast for all 20 industries as we promised in Part 1.

First, we must refit the stack-level weighted average model with the prepared dataset from Part 2. We do this with modeltime_refit().

Then we calculate the Turnover predictions over the next 12 months (values are still transformed). We do this with modeltime_forecast() and by setting new_data to the future dataset.

# Toggle ON parallel processing
plan(
  strategy = cluster,
  workers  = parallel::makeCluster(n_cores)
)

# Refit the model on prepared dataset
tic()
set.seed(123)
refit_stacking_tbl <- calibration_stacking %>% 
  modeltime_refit(
    data = artifacts$data$data_prepared_tbl,
    resamples = artifacts$data$data_prepared_tbl %>%
      drop_na() %>%
      vfold_cv(v = 10)
  )
toc()

# 12-month forecast calculations with future dataset

forecast_stacking_tbl <- refit_stacking_tbl %>%
  modeltime_forecast(
    new_data    = artifacts$data$future_tbl,
    actual_data = artifacts$data$data_prepared_tbl %>%
      drop_na(), 
    keep_data = TRUE
  )

# Toggle OFF parallel processing
plan(sequential)

We invert the Turnover values back to their original values with standardize_inv_vec() and expm1().

Finally, we plot the forecast for the next 12 months within the original scale of the Turnover measure.

lforecasts <- lapply(X = 1:length(Industries), FUN = function(x){
  forecast_stacking_tbl %>%
    filter(Industry == Industries[x]) %>%
    #group_by(Industry) %>%
    mutate(across(.value:.conf_hi,
                  .fns = ~standardize_inv_vec(x = .,
                                              mean = artifacts$standardize$std_mean[x],
                                              sd = artifacts$standardize$std_sd[x]))) %>%
    mutate(across(.value:.conf_hi,
                  .fns = ~expm1(x = .)))
})

forecast_stacking_tbl <- bind_rows(lforecasts)

forecast_stacking_tbl %>%
  group_by(Industry) %>%
  plot_modeltime_forecast(.title = "Turnover 1-year forecast",     
                          .facet_ncol         = 4, 
                          .conf_interval_show = FALSE,
                          .interactive        = TRUE)

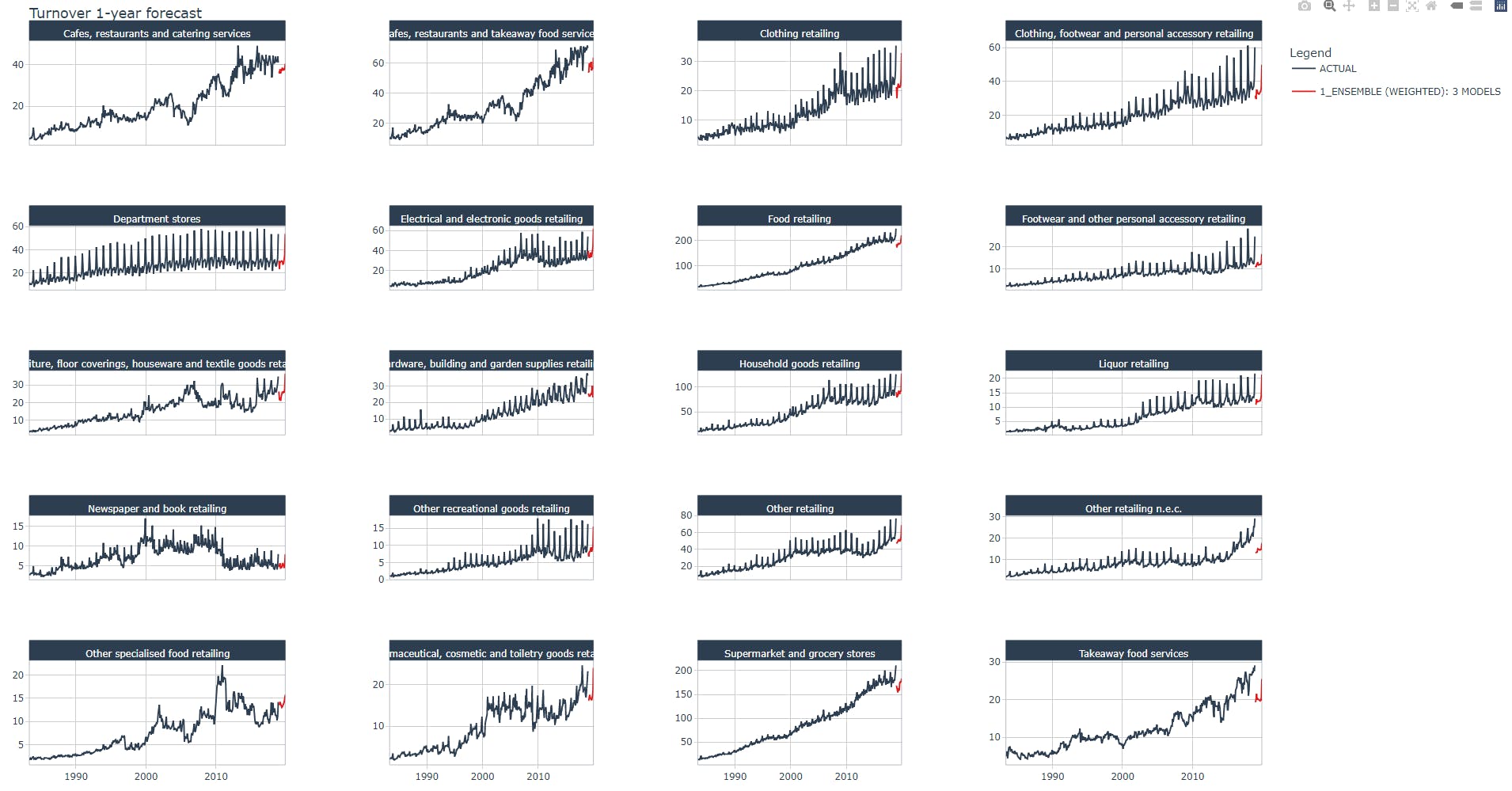
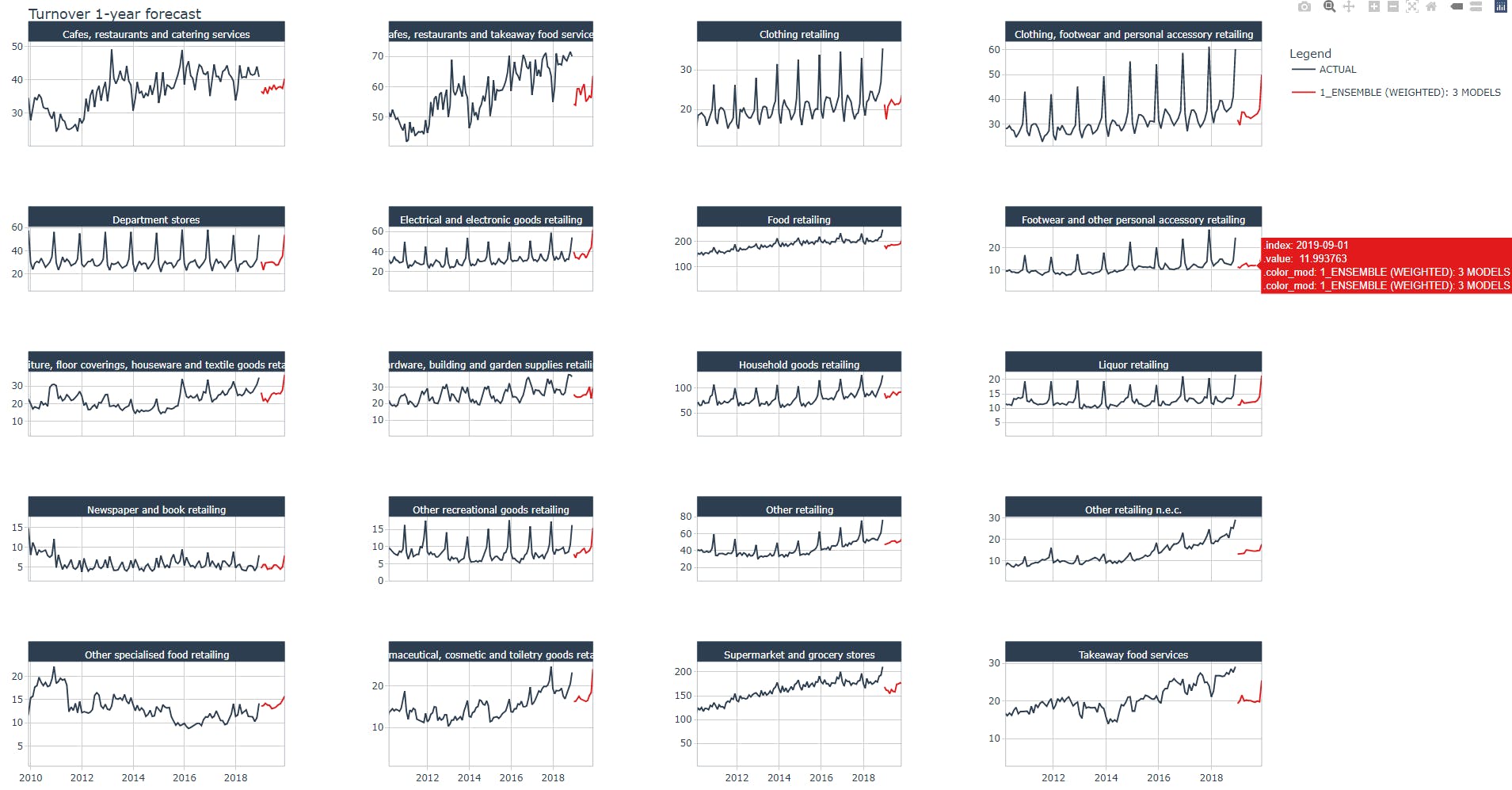
Below a zoomed view of the same plot

Conclusion

In this article you have learned how to implement stacked ensemble models. A stacking algorithm or meta-learner learns from predictions. The predictions come from k-fold cross-validations applied to each submodel. Once fed into the meta-learner tunable specification, a hyperpameter tuning will be peformed for the meta-learner.

We defined three meta-learners: SVM, Random Forest, and XGBoost from which we defined a weighted average ensemble model (stack-level) using the same method as explained Part 5.

The stacked ensemble algorithm outperformed all algorithms.

References

1 Dancho, Matt, "DS4B 203-R: High-Performance Time Series Forecasting", Business Science University

Time Series Forecasting Lab (Part 6) - Stacked Ensembles

Comments (3)