Time Series Forecasting Lab (Part 5)

Cover photo by Hannah Busing on Unsplash

Go to R-bloggers for R news and tutorials contributed by hundreds of R bloggers.

Introduction

This is the fifth of a series of 6 articles about time series forecasting with panel data and ensemble stacking with R.

Through these articles I will be putting into practice what I have learned from the Business Science University training course 1 DS4B 203-R: High-Performance Time Series Forecasting", delivered by Matt Dancho. If you are looking to gain a high level of expertise in time series with R I strongly recommend this course.

The objective of this article is learn how to create average and weighted ensembles using all (both non-tuned and tuned) model from Part 3 and Part 4. We will also check if any of these ensemble models can outperform the tuned Prophet Boost model.

Prerequisites

I assume you are already familiar with the following topics, packages and terms:

dplyr or tidyverse R packages
calibration table from Part 3 and Part 4
model evaluation metrics: RMSE, R-squared, ...

Packages

The following packages must be loaded:

# 01 FEATURE ENGINEERING
library(tidyverse)  # loading dplyr, tibble, ggplot2, .. dependencies
library(timetk)  # using timetk plotting, diagnostics and augment operations
library(tsibble)  # for month to Date conversion
library(tsibbledata)  # for aus_retail dataset
library(fastDummies)  # for dummyfying categorical variables
library(skimr) # for quick statistics

# 02 FEATURE ENGINEERING WITH RECIPES
library(tidymodels) # with workflow dependency

# 03 MACHINE LEARNING
library(modeltime) # ML models specifications and engines
library(tictoc) # measure training elapsed time

# 04 HYPERPARAMETER TUNING
library(future)
library(doFuture)
library(plotly)

# 05 ENSEMBLES
library(modeltime.ensemble)

Load calibration tables

Load all calibration tables for all tuned & non-tuned models we have trained so far, nad remind ourselves of the accuracy results so far:

> calibration_tbl <- read_rds("workflows_NonandTuned_artifacts_list.rds")
> calibration_tbl <- calibration_tbl$calibration
> calibration_tbl %>% 
   modeltime_accuracy() %>%
   arrange(rmse)
# A tibble: 8 x 9
  .model_id .model_desc                       .type   mae  mape  mase smape  rmse   rsq
      <int> <chr>                             <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1         7 PROPHET W/ REGRESSORS             Test  0.189  21.6 0.417  21.5 0.240 0.856
2         3 PROPHET W/ REGRESSORS - Tuned     Test  0.189  21.6 0.418  21.5 0.241 0.857
3         4 PROPHET W/ XGBOOST ERRORS - Tuned Test  0.191  25.7 0.421  19.9 0.253 0.780
4         8 PROPHET W/ XGBOOST ERRORS         Test  0.204  24.8 0.451  20.8 0.287 0.753
5         2 XGBOOST - Tuned                   Test  0.219  23.6 0.482  22.9 0.296 0.762
6         6 XGBOOST                           Test  0.216  25.0 0.476  22.4 0.299 0.747
7         1 RANGER - Tuned                    Test  0.231  26.1 0.509  24.6 0.303 0.766
8         5 RANGER                            Test  0.235  25.4 0.519  25.0 0.312 0.765

Average ensembles

Average ensembles is a fairly simple concept, its main advantage is that it does not require retraining. If you use the mean be aware of the individual performance of each model since the "average model" performance will be sensitive to "bad models" and outliers. To cope with this situation you can use the median (more robust than the mean). Do not use the median when all models are doing pretty well.

To create these two ensembles is pretty simple, all you have to do is to pipe the modeltime table with all workflows into the ensemble_average() and specify the type, either mean or median.

> ensemble_fit_mean <- submodels_tbl %>%
  ensemble_average(type = "mean")

> ensemble_fit_mean
-- Modeltime Ensemble -------------------------------------------
Ensemble of 8 Models (MEAN)

# Modeltime Table
# A tibble: 8 x 5
  .model_id .model     .model_desc                       .type .calibration_data   
      <int> <list>     <chr>                             <chr> <list>              
1         1 <workflow> RANGER - Tuned                    Test  <tibble [1,000 x 4]>
2         2 <workflow> XGBOOST - Tuned                   Test  <tibble [1,000 x 4]>
3         3 <workflow> PROPHET W/ REGRESSORS - Tuned     Test  <tibble [1,000 x 4]>
4         4 <workflow> PROPHET W/ XGBOOST ERRORS - Tuned Test  <tibble [1,000 x 4]>
5         5 <workflow> RANGER                            Test  <tibble [1,000 x 4]>
6         6 <workflow> XGBOOST                           Test  <tibble [1,000 x 4]>
7         7 <workflow> PROPHET W/ REGRESSORS             Test  <tibble [1,000 x 4]>
8         8 <workflow> PROPHET W/ XGBOOST ERRORS         Test  <tibble [1,000 x 4]>

> ensemble_fit_mean <- submodels_tbl %>%
  ensemble_average(type = "median")

-- Modeltime Ensemble -------------------------------------------
Ensemble of 8 Models (MEDIAN)

# Modeltime Table
# A tibble: 8 x 5
  .model_id .model     .model_desc                       .type .calibration_data   
      <int> <list>     <chr>                             <chr> <list>              
1         1 <workflow> RANGER - Tuned                    Test  <tibble [1,000 x 4]>
2         2 <workflow> XGBOOST - Tuned                   Test  <tibble [1,000 x 4]>
3         3 <workflow> PROPHET W/ REGRESSORS - Tuned     Test  <tibble [1,000 x 4]>
4         4 <workflow> PROPHET W/ XGBOOST ERRORS - Tuned Test  <tibble [1,000 x 4]>
5         5 <workflow> RANGER                            Test  <tibble [1,000 x 4]>
6         6 <workflow> XGBOOST                           Test  <tibble [1,000 x 4]>
7         7 <workflow> PROPHET W/ REGRESSORS             Test  <tibble [1,000 x 4]>
8         8 <workflow> PROPHET W/ XGBOOST ERRORS         Test  <tibble [1,000 x 4]>

Weigthed ensembles

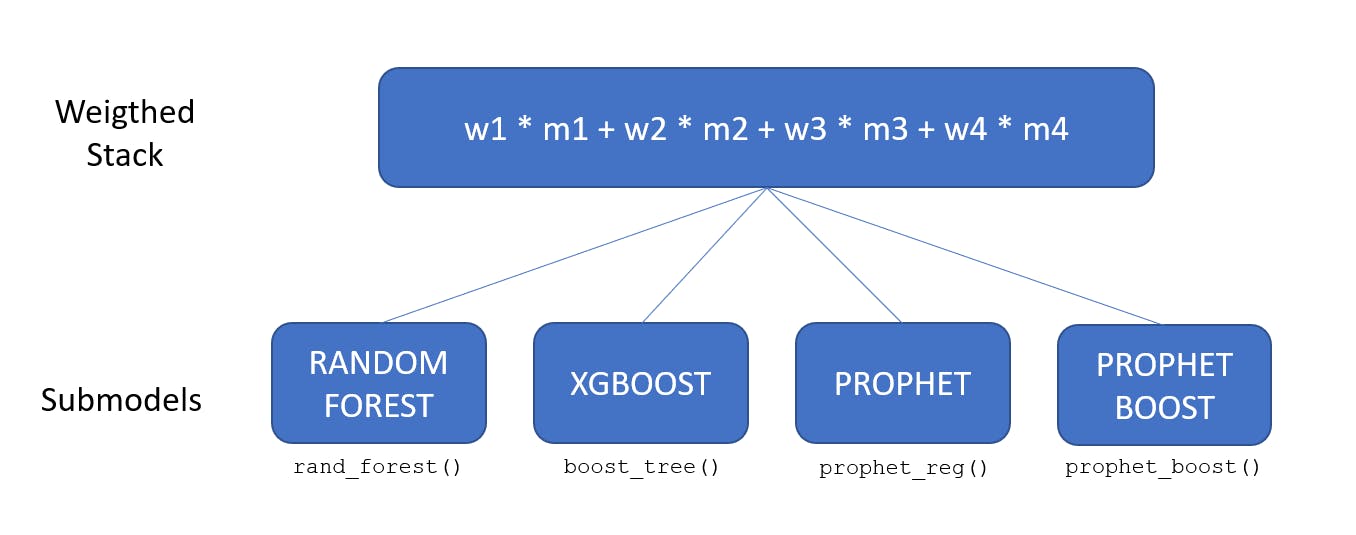
Weighted ensembles can improve performance compared to average ensembles but we must decide of the weight values. One solution is to use a simple rank technique: create a rank column for which highest value is for the best model (lowest RMSE).

In the code snippet below we add the rank column and then we select .model_id and rank columns to define a loadings tibble which will be used for defining the weighted ensemble.

> calibration_tbl %>%
   modeltime_accuracy() %>%
   mutate(rank = min_rank(-rmse)) 
# A tibble: 8 x 10
  .model_id .model_desc                       .type   mae  mape  mase smape  rmse   rsq  rank
      <int> <chr>                             <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int>
1         1 RANGER - Tuned                    Test  0.231  26.1 0.509  24.6 0.303 0.766     2
2         2 XGBOOST - Tuned                   Test  0.219  23.6 0.482  22.9 0.296 0.762     4
3         3 PROPHET W/ REGRESSORS - Tuned     Test  0.189  21.6 0.418  21.5 0.241 0.857     7
4         4 PROPHET W/ XGBOOST ERRORS - Tuned Test  0.191  25.7 0.421  19.9 0.253 0.780     6
5         5 RANGER                            Test  0.235  25.4 0.519  25.0 0.312 0.765     1
6         6 XGBOOST                           Test  0.216  25.0 0.476  22.4 0.299 0.747     3
7         7 PROPHET W/ REGRESSORS             Test  0.189  21.6 0.417  21.5 0.240 0.856     8
8         8 PROPHET W/ XGBOOST ERRORS         Test  0.204  24.8 0.451  20.8 0.287 0.753     5

> loadings_tbl <- submodels_tbl %>%
  modeltime_accuracy() %>%
  mutate(rank = min_rank(-rmse)) %>%
  select(.model_id, rank)

Then the weigths are created by passing models' rank to the ensemble_weighted() function. The newly created ".loadings" column are the weights, the sum of all weigths is equal to 1.

> ensemble_fit_wt <- submodels_tbl %>%
  ensemble_weighted(loadings = loadings_tbl$rank)

> ensemble_fit_wt$fit$loadings_tbl
# Modeltime Table
# A tibble: 8 x 2
  .model_id .loadings
      <int>     <dbl>
1         1    0.0556
2         2    0.111 
3         3    0.194 
4         4    0.167 
5         5    0.0278
6         6    0.0833
7         7    0.222 
8         8    0.139

Models evaluation

Finally, let us display the accuracy results by adding previous ensemble models to a modeltime table, calibrating the latter and piping it into the modeltime_accuracy() function. We sort by ascending RMSE.

modeltime_table(
  ensemble_fit_mean,
  ensemble_fit_median,
  ensemble_fit_wt
) %>%
  modeltime_calibrate(testing(splits)) %>%
  modeltime_accuracy(testing(splits)) %>%
  arrange(rmse)

# A tibble: 3 x 9
  .model_id .model_desc                   .type   mae  mape  mase smape  rmse   rsq
      <int> <chr>                         <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1         3 ENSEMBLE (WEIGHTED): 8 MODELS Test  0.176  20.7 0.388  19.5 0.237 0.840
2         1 ENSEMBLE (MEAN): 8 MODELS     Test  0.189  21.8 0.417  20.6 0.255 0.819
3         2 ENSEMBLE (MEDIAN): 8 MODELS   Test  0.204  23.0 0.450  21.8 0.275 0.797

As per the table below the weighted average ensemble performs better than other two average ensembles.

Let us now check if it performs better than the individual workflows from Part 4.

We add the ensembles' calibration table to the non-tuned and tuned models' calibration table (calibration_tbl).

> calibration_all_tbl <- modeltime_table(
  ensemble_fit_mean,
  ensemble_fit_median,
  ensemble_fit_wt
) %>% 
  modeltime_calibrate(testing(splits)) %>%
  combine_modeltime_tables(calibration_tbl)

> calibration_all_tbl %>%
  modeltime_accuracy() %>%
  arrange(rmse)

# A tibble: 11 x 9
   .model_id .model_desc                       .type   mae  mape  mase smape  rmse   rsq
       <int> <chr>                             <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
 1         3 ENSEMBLE (WEIGHTED): 8 MODELS     Test  0.176  20.7 0.388  19.5 0.237 0.840
 2        10 PROPHET W/ REGRESSORS             Test  0.189  21.6 0.417  21.5 0.240 0.856
 3         6 PROPHET W/ REGRESSORS - Tuned     Test  0.189  21.6 0.418  21.5 0.241 0.857
 4         7 PROPHET W/ XGBOOST ERRORS - Tuned Test  0.191  25.7 0.421  19.9 0.253 0.780
 5         1 ENSEMBLE (MEAN): 8 MODELS         Test  0.189  21.8 0.417  20.6 0.255 0.819
 6         2 ENSEMBLE (MEDIAN): 8 MODELS       Test  0.204  23.0 0.450  21.8 0.275 0.797
 7        11 PROPHET W/ XGBOOST ERRORS         Test  0.204  24.8 0.451  20.8 0.287 0.753
 8         5 XGBOOST - Tuned                   Test  0.219  23.6 0.482  22.9 0.296 0.762
 9         9 XGBOOST                           Test  0.216  25.0 0.476  22.4 0.299 0.747
10         4 RANGER - Tuned                    Test  0.231  26.1 0.509  24.6 0.303 0.766
11         8 RANGER                            Test  0.235  25.4 0.519  25.0 0.312 0.765

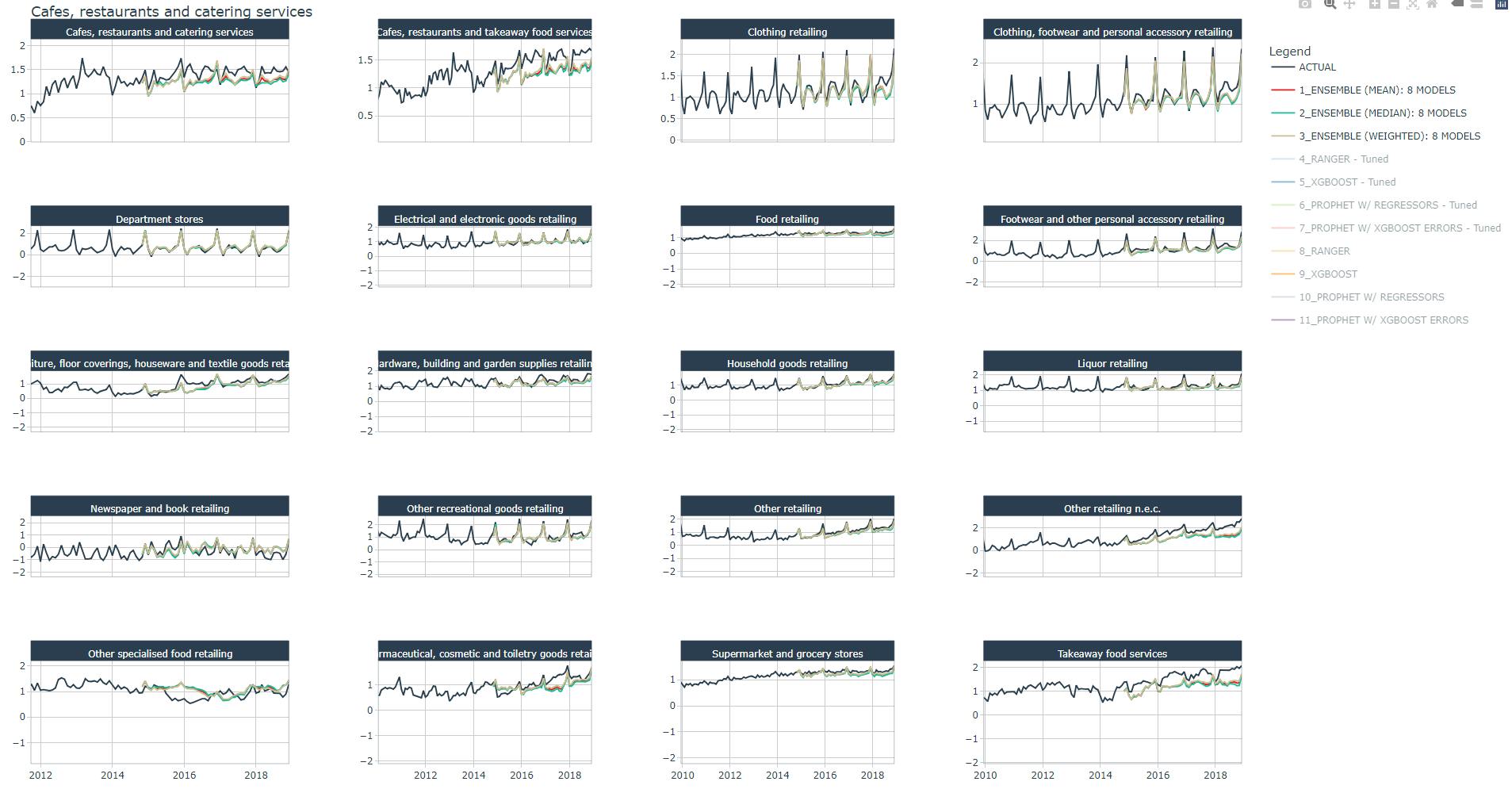
Forescast plot

We have already plotted all tuned and non-tuned models' forecast in Part 4, here we plot only the average ensembles' forecast.

Conclusion

In this article you've learned how to create average (mean or median) ensembles and weighted average ensembles. The latter was created using the rank technique.

Since one of the average ensemble was the best model, we did not bother with improving ensemble models' performance with model selection e.g., selecting the top 5 models and/or suppressing redundant models such as the tuned and non-tuned Prophet models which have the same performance.

In Part 5, we will try to outperform the weighted average ensemble .

References

1 Dancho, Matt, "DS4B 203-R: High-Performance Time Series Forecasting", Business Science University

Time Series Forecasting Lab (Part 5) - Ensembles

Comments