Search for a command to run...
Particle Swarm Optimization with tibbles
No comments yet. Be the first to comment.
Intelligence en essaim, contraintes multi-objectifs, optimisation quantique. L'algorithme confronté aux problèmes que la force brute ne résout pas.
Towards non-dominated particles for MOPSO
Le 16 juin 2026, Arthur Mensch, le patron emblématique de Mistral AI, a publié sur LinkedIn un message d’une rare solennité. Le discours officiel y célèbre, comme toujours, l’indépendance technologiqu
En janvier 2026, la directrice financière d'OpenAI a confirmé un chiffre que personne n'a relevé. Le triplement des revenus de l'entreprise — de 6,7 à 20 milliards de dollars — suit exactement le trip
En moins de trois mois, début 2026, Nvidia a injecté plus de 42 milliards de dollars dans l'écosystème IA. 30 milliards dans OpenAI. 10 milliards dans Anthropic. 2 milliards dans Nebius. Le reste disp
Un ingénieur. Soixante minutes. Un produit SaaS en production, utilisé par 450 marques.
Série "Couche 1 - Les Données"
Cover photo by Eric Ward on Unsplash
Go to R-bloggers for R news and tutorials contributed by hundreds of R bloggers.
This article is the Part 3 of the series (Swarm) Portfolio Optimization. I assume you have read Part 2 - Notion of non-dominated solutions.
Here, I am going to take a step back and resolve a single-objective optimization with a Particle Swarm Optimization (PSO) algorithm before moving forward with multi-objective optimization introduced in Part 2 - Notion of non-dominated solutions.
The proposed code is not an optimized one. I wanted to differentiate this article from other R-related ones by implementing the PSO algorithm with tibbles: saving all the population information at each iteration in this format can be useful if you are willing to e.g., plot dynamic movement of the swarm, and perform further analyses.
This chapter is based on Maurice Leclerc's book "Particle Swarm Optimization" [1]. There are tons of articles and bibliography on PSO and its variants. I will stick to a simple version for PSO, without informants, for the sake of clarity based on the algorithm described in the next chapter.
We are interested only in continuous problems with real variables. A search space is defined, for example, classically, like one (hyper)cube of the form [XMIN, XMAX]^D.
Initialization simply consists of initially randomly placing the particles according to a uniform distribution in this search space.
The particles have velocities. By definition, a **velocity ** is a vector or, more precisely, an operator, which, applied to a position, will give another position. It is in fact a displacement, called velocity because the time increment of the iterations is always implicitly regarded as equal to 1.
For the moment, let us be satisfied with deriving at random the values of the components of each velocity, according to a uniform distribution in:
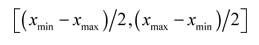
The dimension of the search space is D. Therefore, the current position or location of a particle in this space at the moment t is given by a vector x(t), with D components.
Its current velocity is v(t). The best position or location found up to now by this particle is given by a vector p(t).
Lastly, the best position or location found by informants of the particle is indicated by a vector g(t).
In general, we will write simply x, v, p, and g.
The dth component of one of these vectors is indicated by the index d, for example xd.
With these notations, the equations of motion of a particle are, for each dimension d:
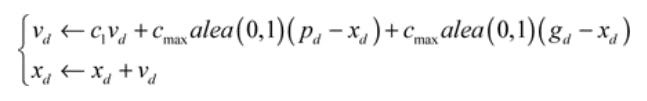
*c1 * is constant (confidence in its own movement) and it will be represented by the VELOCITY_FACTOR constant.
To use this model, the two parameters c1 and cmax (represented by the CMAX constant) must be defined. CMAX can be regarded as the ** maximum confidence granted by the particle to any performance transmitted by another. For each problem, “the right” values can be found only by experiment: both VELOCITY_FACTOR and CMAX must not be chosen independently and the following couple of values are recommended
(VELOCITY_FACTOR = 0.7, CMAX = 1.47)
(VELOCITY_FACTOR =** 0.8**, CMAX = 1.62)
The first product cmax . alea(0,1) in the first equation of motion will be denoted as C1 (confidence granted by the particle to its self-performance), and second one as C2 (confidence granted by the particle to the best particle performance). Note: C2 is supposed to be confidence granted by the particle to its best *informant *performance, but as stated earlier in this article we do not consider Leclerc's implementation with informants.
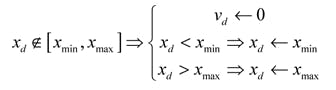
In practice, it is not desirable that too many particles tend to leave the search space as early as the first increment. We supplement the mechanism of **confinement **(which brings back the particle to the border of the search space) with a velocity modification. In this article we choose to perform a velocity component cancellation thus, the complete mechanism is described by the following operations:
This chapter is based on a book Meta-heuristic and Evolutionary Algorithms for Engineering Optimization [2]
Generally speaking, the objective of the PSO algorithm is to minimize a function f(x) where x denotes a particle.
We start with an initial population.
For any particle, a position x is said to be better than a position y if **f(x)<f(y) **.
Now the population is updated by the movement of particles around the search space.
Each particle i remembers the best position Pi attained by it in the past.
Also the swarm remembers the global best value G attained by any particle in the past.
Each particle's movement is determined by its current velocity, its own best known position and the global best value of the swarm.
The swarm is expected to move towards the global best solution or at least towards a satisfactory solution for which the function value is close to the global minimum.
The PSO algorithm implemented in this article is the following:
We will use the same 4-asset portfolio (MSFT, AAPL, GOOG, NFLX) as in Part 2.
The goal is to find the optimal solution (or portfolio weights) for the single-objective optimization problem below. I have strikethrough the second objective function from Part 2, leaving only the minimization of the first objective function: the Value-at-Risk (VaR), relative to the mean, of the portfolio.
Load the same packages as in Part 2
library(PerformanceAnalytics)
library(quantmod)
library(tidyquant)
library(tidyverse)
library(timetk)
library(skimr) # not used in this article
library(plotly) # not used in this article
library(caret) # not used in this article
library(tictoc)
Algorithm steps 1. (population size as NUMBER_PARTICLES) and 5. (w as VELOCITY_FACTOR) will be defined along with the other PSO parameters.
# PSO parameters
NUMBER_OF_ASSETS = 4 # D = 4 dimensions
NUMBER_PARTICLES = 40 # N = population size
VELOCITY_FACTOR = .7 # confidence in its own movement
XMIN = .05 # used for mechanism of confinement, not as constraint
XMAX = .80 # used for mechanism of confinement, not as constraint
CMAX = 1.47 # maximum confidence granted by the particle to any performance transmitted by another
VMAX = (XMAX-XMIN)/2
VMIN = (XMIN-XMAX)/2
MAX_ITERATIONS = 50
As explained in the code snippet below, if you have already saved as returns_daily_tbl.rds the 4 assets daily returns generated in Part 2 chapter "Collect prices, compute daily returns and clean data", you can load it directly and apply the formatTibble() function to generate the returns tibble that will be used in this article.
If you haven't saved the daily returns then run the code snippet in Part 2's chapter "Collect prices, compute daily returns and clean data" and don't forget to apply the formatTibble() function.
## Assets & Daily returns data ----
# Microsoft, Apple, Google, Netflix
assets <- c("MSFT", "AAPL", "GOOG", "NFLX")
returns_daily_tbl <- readRDS("<RDS file path>/returns_daily_tbl.rds")
returns <- returns_daily_tbl %>%
formatTibble()
rm(returns_daily_tbl)
At each iteration the program will generate a tibble with the following format: each line is a particle representing a portfolio of the 4 assets. Since there are 4 assets there will be 4 components for the location, velocity and best location of each particle.
Columns x_1, x_2, x_3, x_4 are the location or position components of the particle.
Column pRelVaR is the "relative to the mean" VaR (see Part 1) calculated with the previous locations (see function computeRelVaR() below).
Columns v_1, v_2, v_3, v_4 are the velocity components of the particle.
Columns p_1, p_2, p_3, p_4 are the best location components of the particle.
The initializePopulation() function applies algorithm steps 2., 3., 4., 6., 7., and it will be run once.
You can save the resulting tibble (with saveRDS for instance) in order to rerun the program several times using the same initial population.
The initializePopulation() function calls the following three functions:
generateRandomLocations(): for steps 2. and 3.
generateRandomVelocities(): for step 4.
computeRelVaR(): for step 7., thus it needs the daily returns tibble.
Step 6. does not need a specific function, all best locationsp_ will be initialized with the initial locations x_ values.
Here's the reference initial population tibble used in this article and for other optimization scenarios e.g., changing parameter couple (VELOCITY_FACTOR, CMAX) and/or population size NUMBER_PARTICLES.
init_pop <- initializePopulation(returns = returns)
> init_pop
# A tibble: 40 x 13
x_1 x_2 x_3 x_4 pRelVaR v_1 v_2 v_3 v_4 p_1 p_2 p_3 p_4
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.137 0.0829 0.392 0.389 1.15 -0.266 -0.0821 0.210 0.245 0.137 0.0829 0.392 0.389
2 0.604 0.106 0.144 0.146 1.10 -0.227 -0.360 -0.350 -0.0668 0.604 0.106 0.144 0.146
3 0.341 0.350 0.176 0.133 1.10 0.257 0.0866 0.122 -0.0764 0.341 0.350 0.176 0.133
4 0.0442 0.449 0.361 0.147 1.13 -0.260 -0.267 0.191 -0.342 0.0442 0.449 0.361 0.147
5 0.144 0.103 0.399 0.355 1.14 -0.0740 -0.224 0.0213 0.155 0.144 0.103 0.399 0.355
6 0.409 0.0956 0.296 0.200 1.10 0.0740 0.310 -0.293 -0.255 0.409 0.0956 0.296 0.200
7 0.0575 0.316 0.198 0.429 1.14 -0.0175 -0.324 -0.106 -0.189 0.0575 0.316 0.198 0.429
8 0.0716 0.363 0.111 0.454 1.14 -0.301 -0.0417 -0.0640 -0.156 0.0716 0.363 0.111 0.454
9 0.0367 0.358 0.425 0.180 1.10 -0.128 -0.129 0.104 -0.293 0.0367 0.358 0.425 0.180
10 0.109 0.164 0.246 0.481 1.18 0.271 -0.0885 -0.160 0.121 0.109 0.164 0.246 0.481
# ... with 30 more rows
initializePopulation <- function(returns){
## Randomly generate locations of particles ----
init_locations <- lapply(X = 1:NUMBER_PARTICLES, function(x){
generateRandomLocations(n = NUMBER_OF_ASSETS, min = XMIN, max = XMAX)
})
init_locations <- init_locations %>%
bind_rows()
## Randomly generate velocities of particles ----
init_velocities <- lapply(X = 1:NUMBER_PARTICLES, function(x){
generateRandomVelocities(n = NUMBER_OF_ASSETS, min = VMIN, max = VMAX)
})
init_velocities <- init_velocities %>%
bind_rows()
## Initialize best locations as first locations ----
init_bestlocations <- init_locations
colnames(init_bestlocations) <- sapply(X = 1:NUMBER_OF_ASSETS, function(x) paste0("p_",x))
## Compute fitness function value, here pRelVaR, for each particle ----
init_particles <- bind_cols(computeRelVaR(tbl = init_locations, returns = returns),
init_velocities)
init_particles <- bind_cols(init_particles, init_bestlocations)
return(init_particles)
}
The function returns a tibble withh n lines, each composed of the x_1, x_2, x_3, x_4 location components randomly generated with the runif() function. The min and max arguments default values will be overwritten with XMIN and XMAX values.
The locations must sum up to 1 (100%) since they represent the weigths of the assets.
generateRandomLocations <- function(n, min=.05, max=.75){
tmp <- runif(n = n, min = min, max = max)
# Weights must sum up to 1 (100%)
nweights <- tmp/sum(tmp)
new_cols <- list()
for(x in 1:n) {
new_cols[[paste0("x_", x, sep="")]] = nweights[x]
}
res <- as_tibble(new_cols)
return(res)
}
The function returns a tibble withh n lines, each composed of the v_1, v_2, v_3, v_4 velocity components randomly generated with the runif() function. The min and max arguments default values will be overwritten with VMIN and VMAX values.
generateRandomVelocities <- function(n, min=-1, max=1){
velocities <- runif(n = n, min = min, max = max)
new_cols <- list()
for(x in 1:n) {
new_cols[[paste0("v_", x, sep="")]] = velocities[x]
}
res <- as_tibble(new_cols)
return(res)
}
The computeRelVaR() function returns a tibble with NUMBER_OF_PARTICLES lines each composed of the x_1, x_2, x_3, x_4 locations and its "relative to the mean" VaR result.
The computeRelVaR() function calls the following three functions:
getWeigthedReturns(): as defined in Part 2
getMeanWeigthedReturns(): as defined in Part 2
getVaRValues(): a simplified version of Part 2's getObjectiveFunctionsValues function, it computes and returns VaR-related values by calling only the objectiveFunction1 as defined in Part 2.
computeRelVaR <- function(tbl, returns){
lrelVaRValues <- lapply(1:nrow(tbl), function(x){
weights <- unlist(tbl[x,c(1:NUMBER_OF_ASSETS)])
returns %>%
getWeigthedReturns(vecA = assets, vecW = weights) %>%
getMeanWeigthedReturns() %>%
getVaRValues(vecW = weights)
})
relVaRValues <- lrelVaRValues %>%
bind_rows() %>%
select(starts_with("x_"), pRelVaR)
return(relVaRValues)
}
The following code snippet implements algorithm step 8.
It simply finds the particle within the initial population that has the **minimum **"relative to the mean" VaR.
g_particle <- init_pop[which(init_pop\(pRelVaR == min(init_pop\)pRelVaR)),]
The code snippet below implements all remaining steps, from 9. to 12.
At each iteration we will save the corresponding population tibble with the iterations_data list. Its initialization is shown in the code snippet below.
iterations_data <- vector("list", MAX_ITERATIONS)
iterations_data[[1]] <- list(pop = init_pop, gb = g_particle)
The main program calls the computeNextLocation() function. This function computes the next location components x_1, x_2, x_3, x_4 based on the velocities v_1, v_2, v_3, v_4 which must be calculated by getVelocityMatrix() based on current best locationsp_1, p_2, p_3, p_4 and global best location.
The new locations tibble will used to calculate the "relative to the mean" VaR (pRelVaR) with the computeRelVaR() function, already described above.
Next, we must identfy if they are any particles with a smaller pRelVaR than the last iteration pRelVaR. If yes, then we must update their best position components p_1, p_2, p_3, p_4 with their new location components x_1, x_2, x_3, x_4, and "rebuild" the population tibble. Else, no best positions will be updated and the same population tibble will be used it next iteration hoping the the randomness introduced in getVelocityMatrix() will generate new locations with smaller pRelVaR.
In either case, we find global best particle with minimum pRelVaR and save it (g_particle). Then, we add the population tibble and globa best particle yo
# Iterations
iter <- 2
while(iter <= MAX_ITERATIONS){
# Compute next velocities and locations
next_locvels <- computeNextLocation(tbl = iterations_data[[iter-1]]\(pop, gbest = iterations_data[[iter-1]]\)gb)
# Get velocities tibble
next_vels <- next_locvels$vels
# Get new locations tibble
next_fitnessval <- computeRelVaR(tbl = next_locvels$locs, returns = returns)
# Get best locations tibble
next_bestloc <- iterations_data[[iter-1]]$pop %>%
select(starts_with("p_"))
# Identify particles with smaller pRelVaR than last iteration pRelVaR
update_idx <- which(next_fitnessval\(pRelVaR < iterations_data[[iter-1]]\)pop$pRelVaR)
# For particles with smaller pRelVaR than last iteration pRelVaR
if(length(update_idx) > 0){
# Update particles' pbest locations (p) with new locations => update pbest tibble
next_bestloc[update_idx, ] <- next_fitnessval[update_idx, -which(colnames(next_fitnessval)=="pRelVaR")]
newRelVaRloc <- computeRelVaR(tbl = next_bestloc, returns = returns)
new_pop <- bind_cols(bind_cols(newRelVaRloc, next_vels), next_bestloc)
}else{
# No updates : did not find particles with smaller pRelVaR than last iteration pRelVaR
new_pop <- iterations_data[[iter-1]]$pop
}
# Find global best particle with minimum pRelVaR
g_particle <- new_pop[which(new_pop\(pRelVaR == min(new_pop\)pRelVaR)),]
iterations_data[[iter]] <- list(pop = new_pop, gb = g_particle)
# iterations_data <- rlist::list.append(iterations_data, it_1 = list(pop = new_pop, gb = g_particle))
iter <- iter + 1
}
# Find particle with solution x_1, x_2, x_3, x_4 with minimum pRelVaR
iterations_data[[MAX_ITERATIONS]]$gb
computeNextLocation() functionIt starts by calling the getVelocityMatrix(), decribed later, which will return particles' velocities as a matrix.
As stated by the second equation of motion, we must sum the velocities matrix to the current locations for which the tibble has been coverted to matrix.
Next, we must verify that the newly calculated locations values stay within the XMIN and XMAX bounds. If not, set its corresponding velocity coordinate to zero and bring the location coordinate value back to its limit, XMIN or XMAX according to the case (new location coordinate < XMIN or > XMAX).
Remember that locations represent the weights of the assets, thus they must sum up to 1 (100%). That is why the simply function asDistribution() is called. This is where I will introduce some flexibility to the algorithm since afetr calling this function you may encounter a location coordinate x_ which is actually smaller than XMIN. See "red" weight vaues in the Excel sheet run results shown at the end of the article.
Both updated locations and velocities matrices will be converted back to tibbles prior being returned within a list.
asDistribution <- function(vec){
vec/sum(vec)
}
computeNextLocation <- function(tbl, gbest){
velmat <- getVelocityMatrix(tbl = tbl, gbest = gbest)
current_mat <- as.matrix(tbl %>% select(starts_with("x_")))
res <- current_mat + velmat
# Verify that weights are within min and max bounds
if (length(which(res < XMIN)) > 0) {
velmat[which(res < XMIN)] = 0L
res[which(res < XMIN)] = XMIN
}
if (length(which(res > XMAX)) > 0) {
velmat[which(res > XMAX)] = 0L
res[which(res > XMAX)] = XMAX
}
# Locations (assets weights) msut sum up to 1
lnorm <- lapply(X = 1:nrow(tbl),
FUN = function(x) asDistribution(res[x,]))
# Convert to tibble
locs <- lnorm %>%
bind_rows() %>%
as_tibble()
vels <- as_tibble(velmat)
colnames(vels) <- sapply(X = 1:NUMBER_OF_ASSETS, FUN = function(x) paste0("v_",x))
# Return tibbles within a list
return(list(locs=locs, vels=vels))
}
getVelocityMatrix() functionHere is where the famous equations of motion (explained above) take place and where randomness is introduced by calculating C1 and C2 parameters.
The getVelocityMatrix() breaks the population tibble into its main components (locations, best locations, and velocities) also as tibbles, and it will extract the best location of the current global best location particle as a vector.
Then the random parameters C1 and C2 will calculated by multiplying fixed parameter CMAX by runif(1, min=0, max=1).
Each particle velocity vetor will be calculated by applying the first equation of motion as R vector operations. The result will be the vector velocities.
We convert the vector velocities into a matrix velmat with number of lines as the number of particles and the number of columns as the number of assets.
Next, we must verify that the newly calculated velocties values stay within the VMIN and VMAX bounds. If not, bring the velocity coordinate back to its limit, VMIN or VMAX, according to the case.
Finally, return the velocities matrix .
getVelocityMatrix <- function(tbl, gbest){
current_tbl <- tbl %>% select(starts_with("x_"))
pbest_tbl <- tbl %>% select(starts_with("p_"))
velocity_tbl <- tbl %>% select(starts_with("v_"))
g <- as.numeric(gbest %>% select(starts_with("p_")))
C1 <- CMAX*runif(1,0,1)
C2 <- CMAX*runif(1,0,1)
velocities <- lapply(X = 1:nrow(tbl), FUN = function(x){
y <- as.numeric(current_tbl[x,])
v <- as.numeric(velocity_tbl[x,])
p <- as.numeric(pbest_tbl[x,])
VELOCITY_FACTOR*v + C1*(p-y) + C2*(g-y)
})
velmat <- matrix(data = as.numeric(unlist(velocities)),
nrow = nrow(tbl),
ncol = NUMBER_OF_ASSETS)
# Setting columns names to "x_" since it will sum with a location matrix
colnames(velmat) <- sapply(X = 1:NUMBER_OF_ASSETS, FUN = function(x) paste0("x_",x))
if (length(which(velmat < VMIN)) > 0) velmat[which(velmat < VMIN)] = VMIN
if (length(which(velmat > VMAX)) > 0) velmat[which(velmat > VMAX)] = VMAX
return(velmat)
}
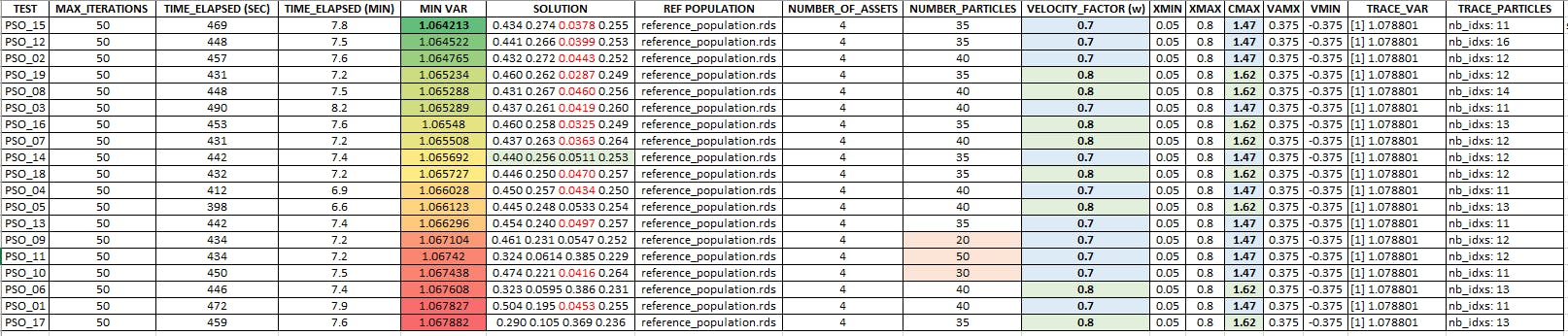
Using the same initial population tibble (inti_pop) I have run 19 optimization scenarios with different population sizes (NUMBER_OF_PARTICLES) and 2 couples of (CMAX, VELOCITY_FACTOR) values.
The **minimum **"relative to the mean" VaR was 1.064213 with following solution of portfolio:
**MSFT **= 0.434 (43.4%)
**APPL **= 0.274 (27.4%)
**GOOG **= 0.0378 (3.78%)
**NFLX **= 0.255 (25.5%)
Below, the results and details of each of the 19 optimization scenarios sorted by ascending "relative to the mean" VaR values.
The "red" values in the portfolios (SOLUTIONS column) below correspond to ones being smaller than XMIN.
This article introduced the basics of the PSO algorithm with tibbles. The goal was to resolve a single-objective optimization problem by minimizing the "relative to the mean" VaR, the objective function.
This version of the algorithm did not use the notion of group of informants per particle (as introduced in [1]) thus, all particles "know" the best global location.
Although location limits XMIN and XMAX were defined we did not use them as optimization constraints. Since the location components (weights of assets) must sum up to 1 (100%) some flexibility was introduced while doing this computation.
In Part 4 we will come back to our multi-objective optimization problem introduced in Part 2 - Notion of non-dominated solutions
[1] Leclerc M., "Particle Swarm Optimization", Lavoisier, 2005
[2] Bozorg-Haddad O., Solgi M., Loaiciga H., "Meta-heuristic and Evolutionary Algorithms for Engineering Optimization"